Introduction

In order to execute a Material Nonlinear Analysis, there must be elastic-plastic material properties assigned to at least one element.

To specify elastic-plastic material properties, select the Material class from the Main Menu Bar and the Material tab will appear (or simply navigate to the Material tab, Define subtab). Select Material: Elastic-Plastic. Decide whether you wish to enter your own material properties, or select material properties from the standard list provided by StressCheck. To use material properties from the standard list, click on the Browser button located at the side of the material ID. A list of material designations will appear in the window of the Material Library form. Then click on the material name to automatically enter the property data in the Material input dialog window and view a plot of the stress-strain relationship. Finally, click on the Accept button to define the material record in your StressCheck session.

For an example of defining/assigning elastic-plastic material properties for a Material Nonlinear Analysis, refer to StressCheck Demo: 3D Material Nonlinear Analysis.

Elastic-Plastic Material Types

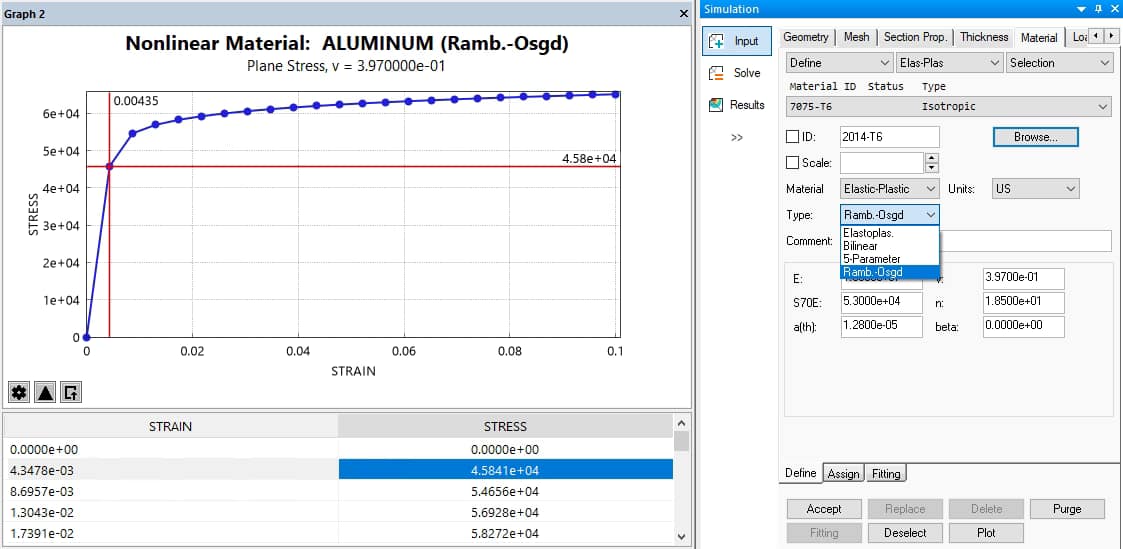
StressCheck supports four types of stress-strain relationships for elastic-plastic materials: Elastoplastic, Bilinear, 5-Parameter, and Ramberg-Osgood. Each of these four stress-strain relationships are uniquely defined by three or more parameters. If the desired material is not present in the Material Library form, then you may manually enter these parameters into the input fields to define your own custom material stress-strain relationship. The stress-strain relationship types, and their respective parameters, are discussed below.

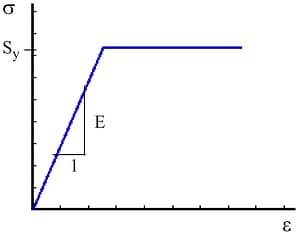
Elastoplastic (Elastoplas.)

Elastoplastic means elastic-ideally-plastic materials. These materials are characterized by three parameters: the modulus of elasticity (E), the Poisson’s ratio (v) and the yield stress (S_y). The stress-strain relationship for an Elastoplastic material is shown in Figure 2:

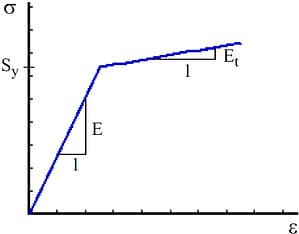
Bilinear

Bilinear means linear-elastic, linear strain-hardening materials, characterized by four parameters: the modulus of elasticity (E), the Poisson’s ratio (v), the yield stress (S_y) and the tangent modulus (E_t) which characterizes strain hardening. The stress-strain relationship for a Bilinear material is shown in Figure 3:

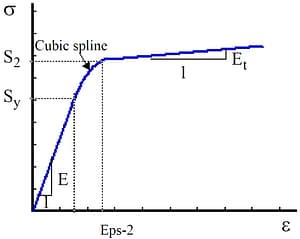
5-Parameter

5-Parameter means that the material is characterized by five parameters: the modulus of elasticity (E), the Poisson’s ratio (v), the yield stress (Sy), the strain-hardening modulus (Et), the starting point on the linear strain-hardening part of the stress-strain relationship given by the strain (Eps-2) which must be greater than Sy/E, and the corresponding stress (S2) which must be greater than Sy. The stress-strain law is linear in the elastic range and for strains greater than Eps-2. The two linear segments are joined by a cubic spline, as shown in Figure 4:

5-Parameter Validation Rules

When a 5-Parameter material nonlinear stress-strain law is defined by the user, the input parameters must meet specific requirements.

Let:

• A(1) = Modulus of Elasticity E at |𝜀| ≤ 𝜀_yield = Sy/E
• A(2) = Modulus Of Elasticity When |𝜀| ≥ Eps-2, 𝐸t
• A(3) = 𝜀_yield = Sy/E
• A(4) = Smallest Epsilon Corresponding To A(2), Eps-2
• A(5) = Smallest Stress Corresponding To A(2), S2

The valid parameter entries for A(1) to A(5) are:

• All values must be positive.
• A(1) should be nonzero.
• A(2) should be less than A(1).
• For a five-parameter curve (A(4) > 0 and A(5) > 0), the following conditions should hold:
  • A(4) should be greater than or equal to A(3).
  • A(5) should be greater than or equal to A(1) * A(4).
  • A(5) should be less than A(1) * A(4).
• If A(4) = A(5) = 0 The 5 parameter curve becomes a 3 Parameter curve (bilinear)

If any of these conditions are not met, the 5-Parameter stress-strain law will not be valid.

Ramberg-Osgood (Ramb.-Osgd)

Ramberg-Osgood materials are characterized by four parameters: the modulus of elasticity (E), the Poisson’s ratio (v), the stress (S_70E), which is the stress corresponding to the intersection of the stress-strain curve with a line which passes through the origin and has the slope of 0.70E, and an exponent (n) in the expression:

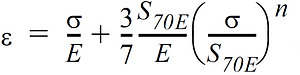
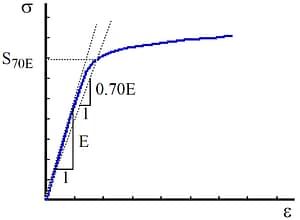
Typical values of n range between 4 and 90 and fractional values are permitted. The corresponding stress-strain curve for a Ramberg-Osgood material is illustrated in Figure 5:

An alternative expression for the Ramberg-Osgood stress-strain curve is given in the MIL-HDBK-5J handbook: Metallic Materials and Elements for Aerospace Vehicle Structures. The expression results in the same stress-strain curve and it is given as:

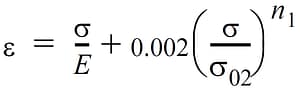
where σ₀₂ is the 0.2% offset yield strength of the material. The relationship between the two set of parameters is the following:

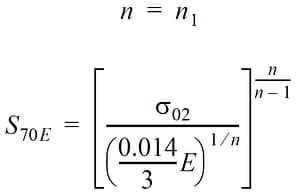
Mix Coefficient, β (Incremental Plasticity)

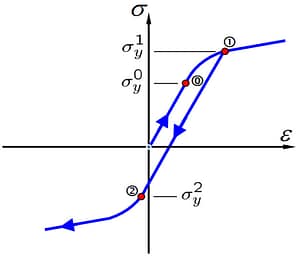
The parameter beta (0<=β<=1) is required for incremental plasticity only, and it is defined as the mixing coefficient between isotropic and kinematic hardening. Note that β = 0 and β = 1 correspond to pure isotropic and pure kinematic hardening rules, respectively (β = 0 is the default value). The mix coefficient β can be obtained from a one dimensional loading and unloading stress-strain curve where the material becomes plastic during loading and reaches the yield limit during unloading, illustrated in Figure 6. From this information, β can be computed as:

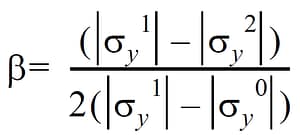
where σ_y0 is the initial proportional limit of the material, σ_y1 is the maximum stress during plastic loading, and σ_y2 is the stress at the limit of the elastic unloading.