Introduction

The two material nonlinear theories implemented in StressCheck are Deformation theory of plasticity (DTP) and Incremental theory of plasticity (ITP). Both require the definition/assignment of elastic-plastic material properties, and the existence of a linear solution.

Definition/Assignment of Elastic-Plastic Materials

In order to perform a material nonlinear (NL Mat) analysis, at least one element must be assigned elastic-plastic material properties. For more information on defining elastic-plastic material properties, refer to Elastic-Plastic Materials.

Obtaining a Linear Solution

Having entered the input data, execute a linear analysis. It is recommended that you obtain a sequence of solutions and estimate the relative error in the energy norm. At least one of the solutions in the sequence should have a small relative error (typically under 1% for 2D-problems and under 5% for 3D-problems).

If this were not the case, then either refine the mesh or increase the polynomial level (or both) and repeat the linear analysis. In general, you should expect the accuracy of the nonlinear solution to be somewhat lower than the accuracy of the linear solution.

Note: in the case of plane strain, axisymmetric, and 3D problems, for example, the plastic strain is subject to the incompressibility constraint, which is not present in the case of the linear solution.

Deformation Theory of Plasticity (DTP)

The implementation is based on the von Mises yield criterion and the deformation theory of plasticity under the assumption of small strain, small displacement for plane-stress, plane-strain, axisymmetric and three-dimensional problems. The purpose and scope of this implementation are as follows:

• Realistic mathematical models of real physical systems must have a capability to provide initial estimates for the effects of nonlinearities at a low computational cost. The deformation theory of plasticity serves this purpose well for a large class of practical problems.
• The effects of a single overload event on structures made of ductile materials are of substantial practical importance. Such effects can be well represented by mathematical models based on the deformation theory of plasticity provided that the plastic flow is contained, that is, the plastic zone is surrounded by elastic material.
• The propagation of cracks in strain-hardening materials is generally correlated with the J-integral. The J-integral is based on the deformation theory of plasticity.
• An important feature of StressCheck is that engineering data can be conveniently extracted from the finite element solutions in the post-solution phase. The deformation theory of plasticity makes it feasible to extend this into the
  elastic-plastic regime because the data storage requirements are small.

Remark: The p-version is not susceptible to Poisson’s ratio locking and hence correct limit loads are obtained. In conventional FEA (h-version) locking occurs when the displacement formulation is used. For this reason alternative formulations, generally known as mixed methods, must be employed.

To solve an elastic-plastic problem, a linear problem must be first solved and an elastic-plastic stress-strain relationship must be specified. With the exception of the material properties, the input data preparation is identical to that for linear problems.

For more information on StressCheck’s implementation of DTP, refer to Numerical Simulation Series: Deformation Theory of Plasticity (DTP) and Notes on Deformation Theory of Plasticity and Geometric Nonlinear Algorithms.

For additional background on DTP, refer to the following:

• Szabó, B. A., Actis, R. L. and Holzer S. M. “Solution of Elastic-Plastic Stress Analysis Problems by the P-Version of the Finite Element Method”, The IMA Volumes in Mathematics and its Applications, Vol. 75, pp. 395-416, 1995.
• Hodge, P. G., Jr. and White, G. N., Jr. “A Quantitative Comparison of Flow and Deformation Theories of Plasticity”, Journal of Applied Mechanics, Vol. 17, pp. 180-184, 1950.
• Budiansky, B. “A Reassessment of Deformation Theory of Plasticity”, Journal of Applied Mechanics, Trans. Am. Soc. Mech. Engrs., Vol 81E, pp. 259-264, 1959.
• Rice, J. R. “A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks”, Journal of Applied Mechanics, Trans. Am. Soc. Mech. Engrs., Vol. 35, pp. 379-386, 1968.
• Nagtegaal, J. C., Parks, D. M. and Rice, J. R. “On Numerically Accurate Finite Element Solutions in the Fully Plastic Range”, Computer Methods in Applied Mechanics and Engineering, Vol. 4, pp. 153-177, 1974.

DTP Material Nonlinear Analysis Setup

Prior to executing a material nonlinear analysis using DTP, you should develop a plan in accordance with the following guidelines:

• Decide what are the data of interest: For example, the limit load, the extent of the plastic zone, the J-integral, strain maxima, etc.
• Decide how accurately you wish to compute the data of interest. If you wish to compute them to less than X percent relative error then the corresponding data in the linear solution should be accurate to within 0.1X and 0.5X. The tolerance selected for the nonlinear solution should be also between 0.1X and 0.5X relative error.
• Make sure that the applied load or imposed displacement will not cause excessive plastic strains, except in the immediate vicinity of singular points. Remember that the small strain, small displacement theory is used. The plastic zone should be completely confined by an elastic zone.

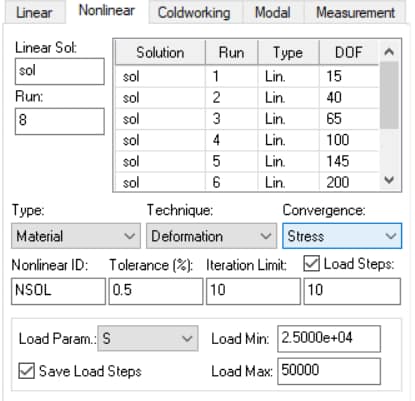
Select the Nonlinear tab in the Solve dialog and the user interface for executing nonlinear solutions will appear. If a linear analysis has already completed, in the scrolling list you will see a list of available linear solutions. Proceed as follows:

• Click on the linear solution which is to be the starting solution for the nonlinear iterations (Linear Sol:). The solution name, run number, type, and associated degrees of freedom (DOF) appear in the scrolling list of the Nonlinear tab. The corresponding discretization will remain fixed in the course of the nonlinear solution process. The relative error in energy norm of the linear solution you select should be small (typically under one percent), and the estimated relative errors in the data of interest should be less than the error tolerance for the nonlinear solution, as explained above.
• Enter a name for the nonlinear solution (Nonlin ID:) which is different from the name of the linear solution (Linear Sol:). For example, you can modify the name of the linear solution by adding the letter N (for nonlinear).
• Select the analysis Type: Material (NL Mat).
• Select the Technique: Deformation, and specify the Convergence option (Stress or Energy) and Tolerance (%). The Convergence options and Tolerance are discussed in the Nonlinear Analysis Overview.
• Select the number of iteration cycles you wish StressCheck to perform automatically and enter this number into the field next to Iteration Limit. StressCheck will stop when the iteration limit is reached, unless the specified error tolerance is reached first. When StressCheck stops at the iteration limit you can examine the results and decide whether to continue or not. If you wish to continue, then simply reset the Iteration Limit and click on the Solve button.
• Optionally, select the Load Steps. This option is used for applying the load in increments from the minimum to the maximum specified load in equal increments. When the Load Steps toggle is turned on, you will be able to select the Load Parameter and enter the maximum value for the load. The minimum load value is displayed but cannot be changed. You also will have the option of selecting the Save Load Steps toggle. This option will save all converged intermediate load steps for further post-processing. Each saved step will be identified with the name given in step 2, an underscore ‘_’ followed by the run number of the starting linear solution. For example, NSOL_8 means that the solution NSOL was initiated from the linear solution #8. The run number associated with each nonlinear solution will correspond to each load step.

For an example of load stepping via DTP, refer to StressCheck Tutorial: Limit Load Analysis via Nonlinear Load Stepping.

Incremental Theory of Plasticity (ITP)

Material nonlinear problems that involve loading conditions that produce stresses outside the quasi-proportional limit (e.g., sequential loading and unloading with reverse plasticity) can be solved using the incremental theory of plasticity (ITP).

The implementation of the ITP is rate (time) independent and considers the von Mises yield criterion and the associated J2 flow rule with isotropic/kinematic (mixed) hardening. Note: the current implementation for plane stress supports kinematic and mixed hardening for bilinear materials only, for all other materials only isotropic hardening is available.

The advantages of the mixed hardening theory over the deformation theory are:

• Allows representation of multiple loading and unloading events, such as those in cold-working simulations.
• It captures the effects of reverse plasticity.
• Describes the hardening behavior of typical engineering materials.

Another important advantage of the ITP for isotropic hardening is that it uses material coefficients derived from a one-dimensional stress-strain curve.

For more information on StressCheck’s implementation of ITP, refer to Incremental Plasticity Hardening Models – An Introduction and Incremental Plasticity Technical Brief.

For additional background on ITP, refer to the following:

• W.F. Chen and D.J. Han. Plasticity for structural engineers. Springer Verlag, New York, ISBN 0-387-96711-7, 1988.
• J.C. Simo and T.J.I. Hughes. Computational Inelasticity. Springer Verlag, New York, ISBN 0-387-97520-9, 1998.
• J.C. Simo and R.L. Taylor. “Consistent Tangent Operators for Rate-Independent Elastoplasticity”. Computer Methods in Applied Mechanics and Engineering, Vol 48, pp. 101-118, 1985.
• J.C. Simo and R.L. Taylor. “A Return Mapping Algorithm for Plane Stress Elastoplasticity”. International Journal for Numerical Methods in Engineering, Vol 22, pp. 649-670, 1986.
• A. Düster and E. Rank. “A p-version finite element approach for two- and three-dimensional problems of the J2 flow theory with nonlinear isotropic hardening”. International Journal for Numerical Methods in Engineering, Vol 53, pp. 49-53, 2002.

Defining Nonlinear Events

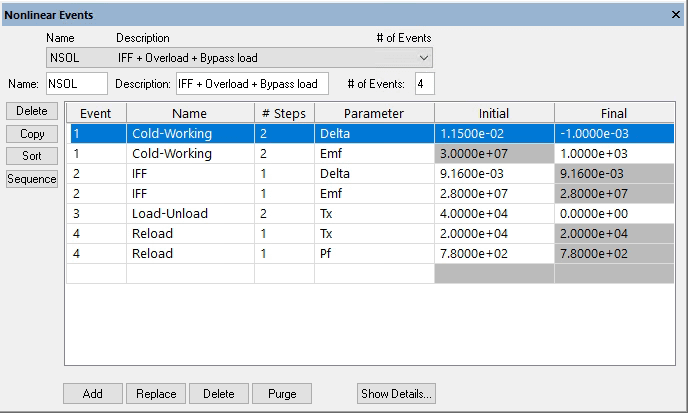
To define nonlinear events for use in ITP analysis (e.g. loading, unloading and reloading events), you may click on the Load Steps button in the Nonlinear tab, or click Edit > Nonlinear Events in the Main Menu (Figure 3). To learn more about defining nonlinear events, refer to the Nonlinear Events Overview.

ITP Material Nonlinear Analysis Setup

Solving a problem using incremental plasticity has similar requirements as those outlined for deformation theory: a linear solution must be solved first and used as the starting point for the nonlinear iterations. Since the quality of the linear solution will determine the quality of the nonlinear solution, it is recommended that a linear solution be selected such that the relative error in energy norm is small (typically under 1% for 2D and 2% for 3D), and the estimated relative errors in the data of interest should be less than the desired error tolerance for the nonlinear solution.

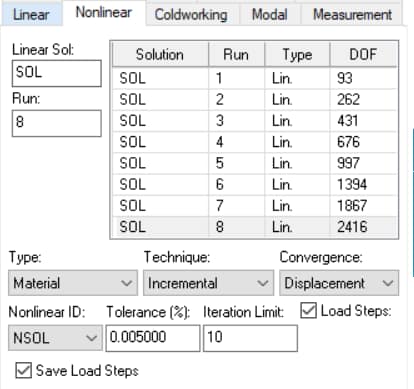
After obtaining a linear solution, select the Nonlinear tab in the Solve dialog and the user interface for executing nonlinear solutions will appear. In the scrolling list you will see the list of linear solutions. Proceed as follows:

• Click on the linear solution which is to be the starting solution for the nonlinear iterations (Linear Sol:). The solution name, run number, type, and associated degrees of freedom (DOF) appear in the scrolling list of the Nonlinear tab. The corresponding discretization will remain fixed in the course of the nonlinear solution process.
• Select the analysis Type: Material (NL Mat).
• Select the Technique: Incremental.
• If a nonlinear events record has not already been defined via the Nonlinear Events dialog, you may define the nonlinear events to be solved by clicking on the Load Steps button and the Nonlinear Events dialog will be displayed. This dialog will be active until dismissed. For more information on defining nonlinear events, refer to the Nonlinear Events Overview.
• Select the name of the nonlinear events record to be computed from the “Nonlin ID:” combo-box. Note: if only one nonlinear events record is defined, it will already be selected in the “Nonlin ID:” combo-box.
• Set the Tolerance (%). The default value for Tolerance is 0.005, and there are two reasons for choosing this value. First, the convergence is computed as the relative difference in displacements between two consecutive solutions, which is similar to convergence in energy. Second, since the error will accumulate between successive load events, a small tolerance value is recommended when using incremental plasticity with more than one load event.
• Set the Iteration Limit. Enter the number of nonlinear iteration cycles you wish to perform automatically (default = 10). StressCheck will stop when the iteration limit is reached, unless the specified error tolerance is reached first. When the solution stops at the iteration limit (without reaching the specified error tolerance) you can examine the results and decide whether to continue or not by increasing the iteration limit. Note: The algorithm implemented for incremental plasticity theory provides a quadratic rate of asymptotic convergence. The default tolerance is normally achieved within the default iteration limit.
• By default, the “Save Load Steps” button is toggled on. This option will save each event and load step solution for post-processing, otherwise only the last converged solution will be available for post-processing.

Load Incrementing

Even though the implemented algorithm for the computation of the nonlinear incremental theory of plasticity allows computing large increments of the applied load, convergence may not be achieved when extremely large load increments are defined. In such cases, the load increment should be reduced for the algorithm to converge. If convergence is not achieved for the first step of the first event, the load has to be reduced by changing the corresponding parameter value in the Parameter pane, and the linear solution has to be recomputed.

Cold Work Simulations

Incremental plasticity can be used to simulate Cold Working operations in 2D and 3D for any number of holes.

• For 2D cases, fastener elements can be used to represent the mandrel interference and subsequent pin loading.
• For 3D cases, the mandrel insertion and removal can be represented using an imposed displacement (radial interference) on nonlinear springs with a spring constant equal to:

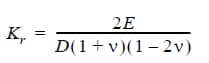
• Where E and are the modulus of elasticity and Poisson’s ratio of the mandrel material, and D is the diameter of the hole. The limitation with this approach is that simulating subsequent loadings on the hole (i.e., pin loads) is complex and could lead to erroneous results as the springs are grounded.

Note that the primary distinction with an analysis using the Coldworking solver and one with incremental plasticity is that reverse plasticity can be represented with incremental plasticity. The Coldworking solver capability is based on the deformation theory of plasticity (DTP) and utilizes linear superposition to obtain the residual stress state therefore it cannot represent reverse plasticity.

For a comparison between isotropic and kinematic hardening for a cold worked hole using ITP, refer to StressCheck Tutorial: Isotropic vs Kinematic Hardening for Cold Worked Holes.

Solution Naming

Each converged saved step will be identified automatically with the name given in step 3 followed by an underscore ‘_’ and the run number of the starting linear solution, a second underscore ‘_’ followed by the sequence number of the load event, and a third underscore ‘_’ followed by the step number of the given load event.

For example, the solution name NLSOL_8_2_1 indicates that the nonlinear solution record NLSOL was initiated from the run #8 of the linear solution, and corresponds to event 2, step 1. The run number associated with each nonlinear solution will correspond to a sequential number that identifies the order in which each nonlinear solution was computed.

3D vs Planar IPT Post-Processing

The main difference between the 3D and 2D (Planar) implementations of incremental plasticity is in the post-processing.

• In 2D the extraction of stresses and equivalent strain is performed by interpolation.
• In 3D however, due to the size of typical problems, the extraction of stresses and equivalent stress is performed by direct evaluation of shape functions fitted during the solution. Fitting of the stress tensor is performed in the least squares sense using continuous shape functions within the element. The fitting error is computed for each element and it is considered to be acceptable if it is within 2%. A message is issued after the completion of the nonlinear incremental solution in case this tolerance is exceeded by any element at any given load event/step. A list with the element number and error for each event/step where the tolerance was exceeded is available in the session log.

Current Limitations

Imposed displacements can be applied during the initial reference condition only. They cannot be modified during subsequent load/unloading events.

For more details on the applicability and scope of ITP, refer to When Is Incremental Plasticity Theory (IPT) a Viable Option?

Executing a Material Nonlinear Analysis

After setting up the material nonlinear analysis in the Nonlinear tab, complete the solution options as follows:

• Select the mode of execution (Execute:). The options are Initialize and Restart. Select “Initialize” when you begin an elastic-plastic analysis. Select “Restart” when you wish to continue from an existing elastic-plastic solution.
• Select Run Mode. The options are Automatic and Stepwise. If you select “Automatic” then the iterations will continue until you reach the specified iteration limit or satisfy the specified error tolerance. If you select “Stepwise” then the iteration process stops after each cycle, and you need to click on the Solve button to go to the next iteration cycle.
• Select Method. StressCheck uses a Direct solver for the solution of linear system of equations.
• Click on the Solve button to start the material nonlinear analysis. When prompted to run the solution again, click “Yes”. Note: to abort the nonlinear solution, press the Esc key or click the Cancel button in the StressCheck Solution Progress dialog.

After the analysis is completed, the nonlinear solution just obtained will be available in the scrolling list of the post-processing dialog box with the name you entered in the Nonlin ID: field, the same run number and DOF as the linear solution selected, and with a type NLMat.

Selecting a different run number of the linear solution to start a nonlinear iteration will result in a new nonlinear solution record with different degrees of freedom and run number than the previous one. Both nonlinear solutions will be available for extraction. You can obtain as many nonlinear solutions as there are linear solutions. In this way you can check the convergence characteristics of the nonlinear solutions.

For an example of setting up and executing a material nonlinear analysis, refer to StressCheck Demo: 3D Material Nonlinear Analysis.