Are Element Distortion Effects Lessened at Higher P-Levels?

Element distortion refers to the difference between the shape of a standard element (a perfect cube in the case of a hexahedral element for example) and the shape of the element in the mesh. The transformation between the standard element and the element in the mesh is called mapping. Mapping functions (Q) establish a relationship between the global coordinates of the element in the mesh (x,y,z) and the local coordinates of the standard element (ξ,η,ζ).

For example, the image below shows how a tetrahedral element in the mesh (right) is mapped from its standard shape (left): 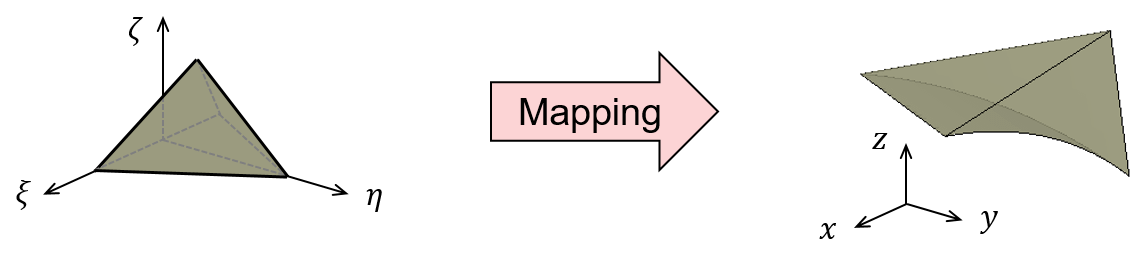In traditional FEA packages, where low order (e.g. p=1 or 2) approximations of the displacement field are used, the effect of distorted elements (or more specifically, distorted tetrahedral elements) is discouraged due to the negative impact of distortion on the quality of the finite element solution. Lower-order implementations are very susceptible to element distortions; as a result, meshes are typically dense.

The implementation of the finite element method in StressCheck is less susceptible to element distortion because the mapping functions and the functions used for the approximation of the displacements are independent. In practice, the elements implemented in StressCheck can be reasonably distorted (e.g. vertex angles in the range 5 ≤ θ ≤ 175, where θ is the solid angle at each corner of the element) and still be acceptable for detailed analysis. Thus, observation of element distortion should not automatically prompt the user to refine the mesh.

However, if the element is too distorted, such as a tetrahedral element with a vanishing angle, the mapping function Q becomes ill-conditioned and its negative impact on solution quality is only partially compensated by the higher polynomial order of approximation of the displacement functions. Since it is not possible to know a-priori the effect of distortion on the quality of the approximation, StressCheck provides for the extraction of every engineering quantity of interest as a function of the number of degrees of freedom (DOF) to check for convergence. Please refer to this article for the recommended quality control procedures in StressCheck.

The following examples demonstrate how auto-meshed tetrahedral elements with reasonable distortion may be used in StressCheck to perform 3D high-quality detailed stress analyses:

• StressCheck Demo: Aircraft Keel Beam Stress Analysis
• StressCheck Demo: 3D Tie Rod Stress Concentration Factor Study

Note: In 3D the use of hexahedral or pentahedral elements is always preferred over tetrahedral elements, as they are more computationally efficient. A user may hand-mesh any part (or automatically mesh constant thickness parts by extrusion) with geometrically mapped hexahedral or pentahedral elements if auto-mesh generated tetrahedral elements are too distorted and convergence checks following p-extension indicate that the errors are larger than what is considered acceptable. For reference, many 3D examples in the StressCheck Handbook folders (Edit > Handbook, click Activate Open File Dialogue to browse the Handbook library) are hand-meshed with hexahedral and/or pentahedral elements.

For complex geometry where the use of automatic mesh generation is the only practical option, local mesh refinement must be used to eliminate highly distorted elements in the regions of primary interest.