
By Dr. Barna Szabó
Engineering Software Research and Development, Inc.
St. Louis, Missouri USA
In my many years of teaching finite element analysis to engineering students, I had to answer many questions about singularities. The usual question, typically in a skeptical tone, was: Are singularities real?
As I was teaching mechanical engineering students, I understood that the question was in the context of continuum mechanics, and the tone suggested that the student found the idea of a material withstanding infinitely large stresses to be utterly absurd. I also understood that he was really interested in knowing why singularities appear in our solutions, and, as a practical matter, what we are supposed to do about them.
I seized such teachable moments to discuss the relationship between mathematical models and physical reality. I explained that a mathematical model is a precisely formulated idea about some specific aspect of physical reality, and should never be confused with reality. Except for marketing pronouncements, there is no such thing as ‘real-world simulation’ or ‘simulating reality’.
Mathematical models are based on certain assumptions which impose limitations on the scope of applicability of the model. For example, models that incorporate the assumptions of linear elasticity, limit strains to be much smaller than unity, the stress is assumed to be proportional to strain, independent of the magnitude of strain, and the material is assumed to be homogeneous. As long as these assumptions are satisfied, the model will make reasonable predictions of deformation and stress distribution. However, the model will produce distorted images of reality when those limitations are exceeded. A common mistake in interpreting model predictions is not taking the limitations of the model into account.
Regarding the practical question of what to do with singularities; we need to distinguish between cases where singularities are just nuisances and where a singularity is the object of simulation.
Singularities as Nuisances
Singularities usually occur due to some minor simplification: For example, in a complicated mechanical or structural component, we may omit fillets, represent the applied forces by point loads, allow abrupt changes in constraint conditions, and so on. In other words, we make the a priori judgment that those simplifications will not significantly influence the quantities of interest.
It is useful to think of the solution domain Ω as consisting of a region of primary interest Ω1 and a region of secondary interest Ω2. The quantities of interest are defined on Ω1. The role of Ω2 is to provide the boundary conditions for Ω1. It is sufficient to ensure that the error, measured in the norm of the formulation, is small on Ω2, a condition that is usually not difficult to satisfy, even when minor features, such as fillets and details of load distribution are omitted.
Using the terminology of structural mechanics, the problem is one of load-displacement relationships on the region of secondary interest, whereas, on the region of primary interest, it is one of strength relationships, that is, the exact values of the quantities of interest have to be finite numbers.
Singularities as the Objects of Simulation
Linear elastic fracture mechanics (LEFM) is an important sub-field of structural mechanics. The goal of the simulation is to predict the size of a crack in a structural or mechanical component, given an initial crack configuration and a load spectrum. Since crack propagation involves highly nonlinear, irreversible processes, it may seem surprising that the predictor can be determined from the stress field of a problem of linear elasticity. A brief explanation follows.
Consider a crack-like notch in an elastic plate, loaded by forces F, as shown in Fig. 1. At the notch tip, the solution of linear elasticity predicts infinitely high stresses. However, pointwise stresses (and strains) have no meaning for real materials. The smallest volume on which stress is meaningfully defined for a real material is the representative volume element (RVE). Failure theories are formulated with reference to stresses or strains averaged over RVEs, not points.
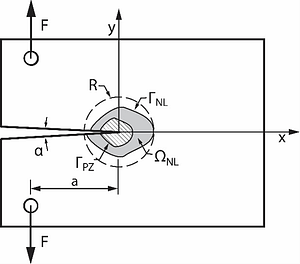
Surrounding the notch tip is a process zone, bounded by the curve ΓPZ shown in Fig 1. In the process zone, large dislocations and voids form and coalesce. These processes are not only outside of the scope of linear elasticity but outside of the scope of continuum mechanics as well. In the zone, labeled ΩNL, continuum mechanics with non-linear material properties is applicable. On and outside of ΓNL the linear theory of elasticity is applicable.
The fundamental modeling assumptions of LEFM are that (a) there is a small circle of radius R, on which the solutions of the nonlinear continuum problem and the linear elasticity problem are virtually identical, and (b) the entire process inside the circle is characterized by the stress intensity factor(s) [1]. These assumptions permit experimental determination of the relationship between crack increments and the difference between the stress intensity factors corresponding to the maximum and minimum load levels in a load cycle, denoted by ΔK. The prediction of crack lengths is based on such empirical relationships.
LEFM models have been validated under constant cycle loading for long cracks in thin plates. Prediction of the growth of small cracks in 3-dimensional stress fields is much more difficult and several ad-hoc procedures are in use [2]. It is safe to say that none of those procedures have been validated under proper validation protocols, such as those outlined in [3].
Conceptual Issues
LEFM is based on the assumption that the driver of crack propagation is a function of the stress intensity factors defined on two-dimensional stress fields. There are two major conceptual problems:
- The relationship between crack increments and ΔK can only be calibrated using 3-dimensional test specimens which have singular points where the crack front intersects the surface of the specimens. Those singularities, not present in two dimensions, influence the relationship between ΔK and the crack increment, hence that relationship is not purely a material property but also depends on the thickness dimension of the test article.
- Application of current LEFM models to very short cracks, such as those that occur at fastener holes in aircraft structures, is highly problematic since the stress field is very different from the two-dimensional stress field on which the stress intensity factors are defined. Other drivers of crack propagation, defined on three-dimensional stress fields, have not been explored. Rather, correction factors have been used. However, the domains of calibration of the correction factors are generally unknown.
We now have reliable methods available to address these issues using the procedures of verification, validation, and uncertainty quantification (VVUQ) [3]. It will take a substantial investment, however, to upgrade the predictive performance of the currently used LEFM models.
References
[1] Szabό, B. and Babuška, I. Finite Element Analysis. Method, Verification, and Validation. John Wiley & Sons, Inc., 2021. [2] AFGROW DTD Handbook. https://afgrow.net/applications/DTDHandbook. [3] B. Szabó and I. Babuška, “Methodology of model development in the applied sciences,” Journal of Computational and Applied Mechanics, vol. 16, no. 2, pp. 75-86, 2021 (open source).Related Blogs:
- Where Do You Get the Courage to Sign the Blueprint?
- A Memo from the 5th Century BC
- Obstacles to Progress
- Why Finite Element Modeling is Not Numerical Simulation?
- XAI Will Force Clear Thinking About the Nature of Mathematical Models
- The Story of the P-version in a Nutshell
- Why Worry About Singularities?
 Serving the Numerical Simulation community since 1989
Serving the Numerical Simulation community since 1989 








Leave a Reply
We appreciate your feedback!
You must be logged in to post a comment.