
By Dr. Barna Szabó
Engineering Software Research and Development, Inc.
St. Louis, Missouri USA
The World-Wide Failure Exercise (WWFE) was an international research project with the goal of assessing the predictive performance of competing failure models for composite materials. Part I (WWFE-I) focused on failure in fiber-reinforced polymer composites under two-dimensional (2D) stresses and ran from 1996 until 2004. Part II was concerned with failure criteria under both 2D and 3D stresses. It ran between 2007 and 2013. Quoting from reference [1]: “Twelve challenging test problems were defined by the organizers of WWFE-II, encompassing a range of materials (polymer, glass/epoxy, carbon/epoxy), lay-ups (unidirectional, angle ply, cross-ply, and quasi-isotropic laminates) and various 3D stress states”. Part III, also launched in 2007, was concerned with damage development in multi-directional composite laminates.
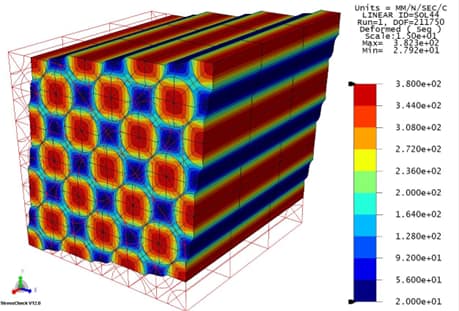
The von Mises stress in an ideal fiber-matrix composite subjected to shearing deformation. The displacements are magnified 15X. Verified solution by StressCheck.
Composite Failure Model Development
According to Thomas Kuhn, the period of normal science begins when investigators have agreed upon a paradigm, that is, the fundamental ideas, methods, language, and theories that guide their research and development activities [2]. We can understand WWFE as an effort by the composite materials research community to formulate such a paradigm. While some steps were taken toward achieving that goal, the goal was not reached. The final results of WWFE-II were inconclusive. The main reason is that the project lacked some of the essential constituents of a model development program. To establish favorable conditions for the evolutionary development of failure criteria for composite materials, procedures similar to those outlined in reference [3] will be necessary. The main points are briefly described below.
- Formulation of the mathematical model: The operators that transform the input data into the quantities of interest are defined. In the case of WWFE, a predictor of failure is part of the mathematical model. In WWFE II, twelve different predictors were investigated. These predictors were formulated based on subjective factors: intuition, insight, and personal preferences. A properly conceived model development project provides an objective framework for ranking candidate models based on their predictive performance. Additionally, given the stochastic outcomes of experiments, a statistical model that accounts for the natural dispersion of failure events must be included in the mathematical model.
- Calibration: Mathematical models have physical and statistical parameters that are determined in calibration experiments. Invariably, there are limitations on the available experimental data. Those limitations define the domain of calibration. The participants of WWFE failed to grasp the crucial role of calibration in the development of mathematical models. Quoting from reference [1]: “One of the undesirable features, which was shared among a number of theories, is their tendency to calibrate the predictions against test data and then predict the same using the empirical constants extracted from the experiments.” ̶ Calibration is not an undesirable feature. It is an essential part of any model development project. Mathematical models will produce reliable predictions only when the parameters and data are within their domains of calibration. One of the important goals of model development projects is to ensure that the domain of calibration is sufficiently large to cover all applications, given the intended use of the model. However, calibration and validation are separate activities. The dataset used for validation has to be different from the dataset used for calibration [3]. Predicting the calibration data once calibration was performed cannot lead to meaningful conclusions regarding the suitability or fitness of a model.
- Validation: Developers are provided complete descriptions of the validation experiments and, based on this information, predict the probabilities of the outcomes of validation experiments. The validation metric is the likelihood of the outcomes.
- Solution verification: It must be shown that the numerical errors in the quantities of interest are negligibly small compared to the errors in experimental observations.
- Disposition: Candidate models are ranked based on their predictive performance, measured by the ratio of predicted to realized likelihood values. The calibration domain is updated using all available data. At the end of the validation experiments, the calibration data is augmented with the validation data.
- Data management: Experimental data must be collected, curated, and archived to ensure its quality, usability, and accessibility.
- Model development projects are open-ended: New ideas can be proposed anytime, and the available experimental data will increase over time. Therefore, no one has the final word in a model development project. Models and their domains of calibration are updated as new data become available.
The Tale of Two Model Development Projects
It is interesting to compare the status of model development for predicting failure events in composite materials with linear elastic fracture mechanics (LEFM), which is concerned with predicting crack propagation in metals, a much less complicated problem. Although no consensus emerged from WWFE-II, there was no shortage of ideas on formulating predictors. In the case of LEFM, on the other hand, the consensus that the stress intensity factor is the predictor of crack propagation emerged in the 1970s, effectively halting further investigation of predictors and causing prolonged stagnation [3]. Undertaking a model development program and applying verification, validation, and uncertainty quantification procedures are essential prerequisites for progress in both cases.
Two Candid Observations
Professor Mike Hinton, one of the organizers of WWFE, delivered a keynote presentation at the NAFEMS World Congress in Boston in May 2011 titled “Failure Criteria in Fibre Reinforced Polymer Composites: Can any of the Predictive Theories be Trusted?” In this presentation, he shared two candid observations that shed light on the status of models created to predict failure events in composite materials:
- “The theories coded into current FE tools almost certainly differ from the original theory and from the original creator’s intent.” – In other words, in the absence of properly validated and implemented models, the predictions are unreliable.
- Disclosed that Professor Zvi Hashin declined the invitation to participate in WWFE-I, explaining his reason in a letter. He wrote: “My only work in this subject relates to unidirectional fibre composites, not to laminates” … “I must say to you that I personally do not know how to predict the failure of a laminate (and furthermore, that I do not believe that anybody else does).”
Although these observations are dated, I believe they remain relevant today. Contrary to numerous marketing claims, we are still very far from realizing the benefits of numerical simulation in composite materials.
A Sustained Model Development Program Is Essential
To advance the development of design rules for composite materials, stakeholders need to initiate a long-term model development project, as outlined in reference [3]. This approach will provide a structured and systematic framework for research and innovation. Without such a coordinated effort, the industry has no choice but to rely on the inefficient and costly method of make-and-break engineering, hindering overall progress and leading to inconsistent results. Establishing a comprehensive model development project will create favorable conditions for the evolutionary development of design rules for composite materials.
The WWFE project was large and ambitious. However, a much larger effort will be needed to develop design rules for composite materials.
References
[1] Kaddour, A. S., and Hinton, M. J. Maturity of 3D Failure Criteria for Fibre-Reinforced Composites: Comparison Between Theories and Experiments: Part B of WWFE-II,” J. Comp. Mats., 47, 925-966, 2013.[2] Kuhn, T. S., The structure of scientific revolutions. Vol. 962. University of Chicago Press, 1997.[3] Szabó, B. and Actis, R. The demarcation problem in the applied sciences. Computers and Mathematics with Applications, Vol. 162, pp. 206–214, 2024.Related Blogs:
- Where Do You Get the Courage to Sign the Blueprint?
- A Memo from the 5th Century BC
- Obstacles to Progress
- Why Finite Element Modeling is Not Numerical Simulation?
- XAI Will Force Clear Thinking About the Nature of Mathematical Models
- The Story of the P-version in a Nutshell
- Why Worry About Singularities?
- Questions About Singularities
- A Low-Hanging Fruit: Smart Engineering Simulation Applications
- The Demarcation Problem in the Engineering Sciences
- Model Development in the Engineering Sciences
- Certification by Analysis (CbA) – Are We There Yet?
- Not All Models Are Wrong
- Digital Twins
- Digital Transformation
- Simulation Governance
- Variational Crimes
- The Kuhn Cycle in the Engineering Sciences
- Finite Element Libraries: Mixing the “What” with the “How”
 Serving the Numerical Simulation community since 1989
Serving the Numerical Simulation community since 1989 






Leave a Reply
We appreciate your feedback!
You must be logged in to post a comment.