By Dr. Barna Szabó
Engineering Software Research and Development, Inc.
St. Louis, Missouri USA

I never understood the statement: “All models are wrong, but some are useful”, attributed to George E. P. Box, a statistician, quoted in many papers and presentations. If that were the case, why should we try to build models and how would we know when and for what purposes they may be useful? We construct models with the objective of making reliable predictions, the degree of reliability being comparable to that of a physical experiment.

Consider, for example, the problem in Fig. 1 showing a sub-assembly of an aircraft structure. The quantity of interest is the margin of safety: Given multiple load conditions and design criteria, estimate the minimum value of the margin of safety and show that the numerical approximation error is less than 5%.   We must have sufficient reason to trust the results of simulation tasks like this.

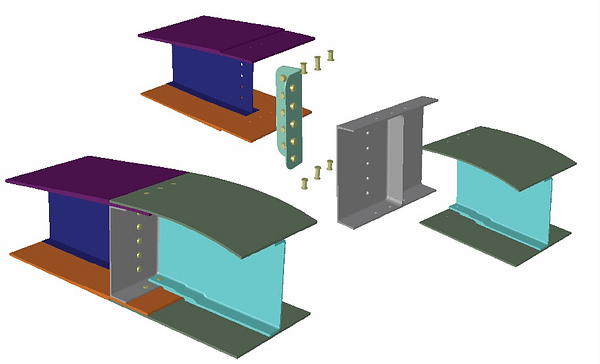
Trying to understand what George Box meant, I read the paper in which he supposedly made the statement that all models are wrong[1] but I did not find it very enlightening. Nor did I find that statement in its often-quoted form. What I found is this non sequitur: “Since all models are wrong the scientist must be alert to what is importantly wrong.” This makes the matter much more complicated: Now we have to classify wrongness into two categories: important and unimportant. By what criteria? – That is not explained.

Box did not have the same understanding as we do of what a mathematical model is. This is evidenced by the sentence: “In applying mathematics to subjects such as physics or statistics we make tentative assumptions about the real world which we know are false but which we believe may be useful nonetheless.” Our goal is not to model the “real world”, a vague concept, but to model specific aspects of physical reality, the quantities of interest having been clearly defined as, for example, in the case of the problem shown in Fig. 1. Our current understanding of mathematical models is based on the concept of model-dependent realism which was developed well after Box’s 1978 paper was written.

Model-Dependent Realism

The term model-dependent realism was introduced by Stephen Hawking and Leonard Mlodinow in their 2010 book, The Grand Design [2] but the distinction between physical reality and ideas of physical reality is older. For example, Wolfgang Pauli wrote in 1948: “The layman always means, when he says `reality’ that he is speaking of something self-evidently known; whereas to me it seems the most important and exceedingly difficult task of our time is to work on the construction of a new idea of reality.” [From a letter to Markus Fierz.]

If two different models describe a set of physical phenomena equally well then both models are equally valid: It is meaningless to speak about “true reality”. In Hawking’s own words [3]: “I take the positivist viewpoint that a physical theory is just a mathematical model and that it is meaningless to ask whether it corresponds to reality. All that one can ask is that its predictions should be in agreement with observation.” In other words, mathematical models are, essentially, phenomenological models.

What is a Mathematical Model?

A mathematical model is an operator that transforms one set of data D, the input, into another set, the quantities of interest F. In shorthand notation we have:

\boldsymbol D\xrightarrow[(I,\boldsymbol p)]{}\boldsymbol F,\quad (\boldsymbol D, \boldsymbol p) \in ℂ \quad (1)

where the right arrow represents the mathematical model. The letters I and p under the right arrow indicate that the transformation involves an idealization (I) as well as parameters (physical properties) p that are determined through calibration experiments. Restrictions on D and p define the domain of calibration ℂ. The domain of calibration is an essential feature of any mathematical model [4], [5].

Most mathematical models used in engineering have the property that the quantities of interest F continuously depend on D and p. This means that small changes in D and/or p will result in correspondingly small changes in F which is a prerequisite to making reliable predictions.

To ensure that the predictions based on a mathematical model are reliable, it is necessary to control two types of error: The model form error and the numerical approximation errors.

Model Form Errors

The formulation of mathematical models invariably involves making restrictive assumptions such as neglecting certain geometric features, idealizing the physical properties of the material, idealizing boundary conditions, neglecting the effects of residual stresses, etc. Therefore, any mathematical model should be understood to be a special case of a more comprehensive model. This is the hierarchic view of models.

To test whether a restrictive assumption is acceptable for a particular application, it is necessary to estimate the influence of that assumption on the quantities of interest and, if necessary, revise the model. An exploration of the influence of modeling assumptions on the quantities of interest is called virtual experimentation [6]. Simulation software tools must have the capability to support virtual experimentation.

Approximation Errors

Approximation errors occur when the quantities of interest are estimated through a numerical process.  This means that we get a numerical approximation to F, denoted by F_num. It is necessary to show that the relative error in F_num does not exceed an allowable value τ_all:

| \boldsymbol F - \boldsymbol F_{num} |/|\boldsymbol F| \le \tau_{all} \quad (2)

This is the requirement of solution verification. To meet this requirement, it is necessary to obtain a converging sequence of numerical solutions with respect to increasing degrees of freedom [6].

Model Development Projects

The formulation of mathematical models is a creative, open-ended activity, guided by insight, experience, and personal preferences. Objective criteria are used to validate and rank mathematical models [4], [5]. 

Model development projects have been classified as progressive, stagnant, and improper [5]. A model development project is progressive if the domain of calibration is increasing, stagnant if the domain of calibration is not increasing, and improper if one or more algorithms are inconsistent with the formulation or the problem-solving method does not have the capability to estimate and control the numerical approximation errors in the quantities of interest. The most important objective of simulation governance is to provide favorable conditions for the evolutionary development of mathematical models and to ensure that the procedures of verification, validation and uncertainty quantification (VVUQ) are properly applied.

Not All Models Are Wrong, but Many of Them Are…

Box’s statement that all models are wrong is not correct. Models, developed under the discipline of VVUQ, can be relied on to make correct predictions within their domains of calibration. However, model development projects lacking the discipline of VVUQ tend to produce wrong models. And there are models, not tethered to scientific principles and methods, that are not even wrong.

References

Related Blogs:

• Where Do You Get the Courage to Sign the Blueprint?
• A Memo from the 5th Century BC
• Obstacles to Progress
• Why Finite Element Modeling is Not Numerical Simulation?
• XAI Will Force Clear Thinking About the Nature of Mathematical Models
• The Story of the P-version in a Nutshell
• Why Worry About Singularities?
• Questions About Singularities
• A Low-Hanging Fruit: Smart Engineering Simulation Applications
• The Demarcation Problem in the Engineering Sciences
• Model Development in the Engineering Sciences
• Certification by Analysis (CbA) – Are We There Yet?