Contrary to popular opinion, Finite Element Modeling is not Numerical Simulation. It was not until the 1980’s that Numerical Simulation was implemented in the technology base of FEA.
A Brief History of FEA
Learn more below about the evolution of Numerical Simulation in FEA, starting in the 1950’s and continuing to the present day.
The first paper on the finite element method (FEM) was published by Turner, M. J., Clough, R. W., Martin H. C. and Topp, L. J. in 1956. From Wikipedia (on Clough):
His article in 1956 was one of the first applications of this computational method. He coined the term “finite elements” in an article in 1960.
Turner, M. J., Clough, R. W., Martin H. C. and Topp, L. J. Stiffness and Deflection Analysis of Complex Structures . Journal of the Aeronautical Sciences, Vol. 23 No. 9, 1956 pp. 805-823.
In 1965, NASA issued a request for a proposal for the development of a structural analysis software tool. The result of this was NASTRAN (NASA Structural Analysis), which implemented the available FEM technology to solve structural problems.
Dr. O.C. Zienkiewicz publishes the first text on the finite element method, called ‘The Finite Element Method’. To this day, it remains a standard reference text for the basis of the FEM.
Computer Sciences Corporation (CSC) released to NASA a FEA program called NASTRAN.
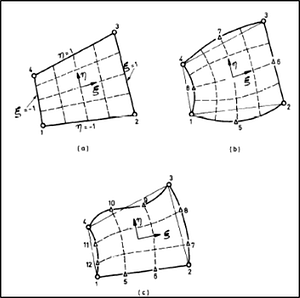
I. Ergatoudis, B. M. Irons and O. C. Zienkiewicz introduced “isoparametric’ mapping for quadrilateral elements. This implied that for a given element, the basis functions used for displacements are the same as the basis functions used for mappings.
Ergatoudis, I., Irons, B. M., and Zienkiewicz, O. C. (1968). Curved, isoparametric,“quadrilateral” elements for finite element analysis. International Journal of Solids and Structures, 4(1), 31-42.
In the late 1960’s, the MacNeal-Schwendler Corporation initiated the first commercially available version of NASTRAN, and dubbed it MSC/NASTRAN. This would be known as the first generation of FEA software.
With the commercialization of FEA taking off, many analysts were no longer aware of the conceptualization errors that can arise when performing simulations with the FEM. For example, combining 1-D and 3-D theories in the same mathematical model. This practice led to unknown uncertainties, and became known as finite element modeling.
The first mathematical proofs on the properties of the FEM were published by I. Babuska and A. K. Aziz, and titled ‘Lectures on mathematical foundations of the finite element method’. Up until now, the FEM was implemented but was not mathematically proven (for example, uniqueness and proof of convergence).
In 1977, Dr. Alberto Peano of Istituto Sperimentale Modelli e Strutture (ISMES) initiated the development of the first professional FEA code based on the p-version of the FEM, called FIESTA. His mission was to perform numerical analysis of dams and other major civil structures. FIESTA would be the second generation of FEA software.
In August of 1979, applied mathematician Dr. Ivo Babuska would write Dr. Barna Szabo and state: ‘…I did go through my manuscript about p-convergence and found everything OK. So I believe that the problem is solved in the sense that it justifies your results theoretically…”. Dr. Babuska would later become a frequent collaborator with Dr. Szabo, and would help blaze a path toward proving mathematically the p-version of FEM (see 1981 for details).
The mathematical proof of p-convergence was performed by I. Babuska, B. A. Szabo and I. N. Katz and published in the SIAM Journal on Numerical Analysis Vol. 18, No. 3 (Jun., 1981), pp. 515-545.
Washington University Technology Associates (WUTA), led by Mr. Brett Taylor and Dr. Barna Szabo, partners with Dr. Alberto Peano of the Experimental Institute for Models and Structures (ISMES), and the McDonnell Douglas Automation Co. to market FIESTA. FIESTA ‘is a mathematical model which makes extensive use of computer graphics for the design of general structures ranging from dams and nuclear pressure vessels to piping systems and machine components.’
St. Louis Globe Democrat
A new p-version FEA code, called PROBE, was developed by Dr. Barna Szabo and Mr. Kent Myers at the Center for Computational Mechanics in Washington University, St. Louis. The purpose of this code would be to provide an ‘industrial-worthy’ implementation of p-version FEA suitable for both research and professional aerospace applications. This is considered the third generation of FEA software.
In 1984, Dr. Barna Szabo, Mr. Brett Taylor, and others formed Noetic Technologies in St. Louis, MO. The goal of this company was to acquire and privately commercialize PROBE for more widespread use.
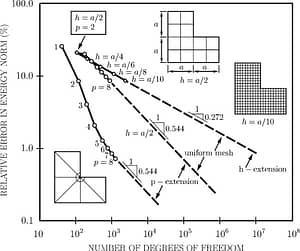
The first demonstration of an exponential rate of convergence using the p-version of the FEM was provided by Drs. Ivo Babuska and Barna Szabó. Up until then, convergence was assumed to be linear in a log-log scale as DOF were increased.
Additionally, superconvergent extraction of stress intensity factors was developed and implemented (see 1988 for more details).
PROBE is commercially released, making it the second professional implementation of the p-version (after FIESTA in 1977), and ultimately the third generation of FEA software. By this time, PROBE had become heavily utilized at the McDonnell Aircraft Company in St. Louis.
In 1987, the RASNA Corporation was founded in San Jose, CA and shortly thereafter began development of MECHANICA. Like predecessors FIESTA and PROBE, MECHANICA was based on the p-version of the FEM. This would become the fourth generation of FEA software.
The first proof of using the contour integral method (CIM) to compute superconvergent extractions of stress intensity factors (SIFs) via p-extension was published by Drs. Barna Szabó BA and Ivo Babuska. This was titled ‘Computation of the amplitude of stress singular terms for cracks and reentrant corners.’ The paper can be located in the following ASTM STP:
In Fracture Mechanics: Nineteenth Symposium ASTM STP 969. T.~A.~Cruse, Ed., American Society for Testing and Materials, Philadelphia (1988) 101–124.
In 1989, the rights for PROBE were purchased by the MacNeal-Schwendler Corporation (MSC). A subsequent p-version implementation into MSC Nastran was performed, but largely unsuccessful due to a ‘square peg/round hole’ approach.
ESRD was founded in 1989 by Barna Szabo, Ivo Babuska and Kent Myers with the principal goal being to develop and commercialize the results of the AFOSR-sponsored research performed at the Center for Computational Mechanics (CCM) of Washington University in St. Louis. This research focused on the p-version of the FEM, and the commercialization would later be called StressCheck.
The first implementation of model hierarchies in FEA software was successfully completed. This meant that for the first time in FEA history, an analyst could separate errors of discretization and idealization. This is essential for verification, validation and uncertainty quantification (VVUQ).
In 1991, Drs. Barna Szabo and Ivo Babuska published ‘Finite Element Analysis’ (John Wiley & Sons, ISBN: 978-0-471-50273-9). This text focused on the implementation and application of the FEM with a focus on solution verification. This text would set a new standard for rigorous implementation of the p-version of the FEM.
From Wiley’s website description: Covers the fundamentals of linear theory of finite elements, from both mathematical and physical points of view. Major focus is on error estimation and adaptive methods used to increase the reliability of results. Incorporates recent advances not covered by other books.
The fifth, and current, generation of commercially available FEA software, StressCheck, is released for the Windows OS. StressCheck set a new standard for hierarchic modeling and error control in numerical simulation.

StressCheck Professional
Parametric Technology Corporation acquired MECHANICA from Rasna Corporation in 1995, and would incorporate the technology into Pro/ENGINEER.
After an extensive study, in 1999 the Composites Affordability Initiative (CAI) committee ‘unanimously’ chose StressCheck as the best software tool to replace existing standard tools used for the analysis of bonded composite aircraft structures.
In 2001, Alexander Düster and E. Rank published “The p-version of the finite element method compared to an adaptive h-version for the deformation theory of plasticity’ (Comput.Methods Appl.Mech.Engng. 190 (2001) 1925-1935). From the abstract:
‘A p-version of the finite element method is applied to the deformation theory of plasticity and the results are compared to a state-of-the-art adaptive h-version. It is demonstrated that even for nonlinear elliptic problems the p-version is a very efficient discretization strategy.’
In 2006, the ASME guide for Verification and Validation in Computational Solid Mechanics was released. This guide was groundbreaking as it laid a foundation for requirements in controlling errors in numerical simulations. StressCheck is the only tool to meet the requirements.
In 2008, NASA released a standard for the development of models and simulations:
‘The standard consists of two parts. The first is the traditional requirements section addressing programmatics,
development, documentation, verification, validation, and the reporting of results from both the M&S analysis and the
examination of compliance with this standard. The second part is a scale for evaluating the credibility of model and
simulation results using levels of merit associated with 8 key factors.’
Therefore, any FEA simulation must past strict requirements of verification to meet compliance. StressCheck is the only tool to meet these requirements.
In 2011, Drs. Barna Szabo and Ivo Babuska published a follow-up to their 1991 text ‘Finite Element Analysis’ with ‘Introduction to Finite Element Analysis’. This text was published as a teaching companion, as well as a learning aid, for both educators, students and professionals.
StressCheck 9.2 sets new standards for detail modeling of composites and providing the highest fidelity of computed information in the industry. StressCheck is the only FEA tool that was developed with an infrastructure that supports verification and validation of computed information.
In 2012, Drs. Barna Szabo and Ricardo Actis of ESRD, Inc. published the first known document detailing simulation governance. This was titled ‘Simulation governance: Technical requirements for mechanical design’, and was published in Comput. Methods Appl. Mech. Engrg. 249-252 (2012) 158-168.
The term simulation governance refers to procedures established for the purposes of ensuring and enhancing the reliability of predictions based on numerical simulation.
Released in 2012, the StressCheck 10 Handbook framework was designed to set a new paradigm for standardization. For the first time in history, there could be proper, site-wide deployment of verified solutions for parameterized problems obtained by numerical means (FEA).
This revolutionary concept would usher in the era of ESRD Smart Apps, which make it possible to standardize recurrent analysis tasks utilizing FEA-based tools with confidence, and develop standard solutions well outside the scope of those available in traditional engineering handbooks.
On June 16, 2014, ESRD released StressCheck v10.1. This is the first fully 64-bit professional version of StressCheck. Major enhancements included an intuitive file system, residual stress module, fracture mechanics and laminated composites upgrades, and improved stability.
Is StressCheck the Right FEA Tool for Me?

ESRD continues to develop & implement powerful features in support of engineers performing detailed stress, strength, damage tolerance, fracture, laminated composites, residual stress, and other analyses requiring high-fidelity FEA simulations.
Looking for Resources?
Recent News & Events
Quick Links
Testimonials
-
“As frequent StressCheck users we rely on the capabilities and reliability of the program to complete our everyday jobs ensuring safe reliable flights of our aircraft. The layout of the program and documentation allow for a quick learning process and the support ESRD offers is second to none. They take the time to answer the most basic questions as well as working through complex problems to ensure the proper validation of results. The effort they make in satisfying their users needs increase the reliability, functionality, and capability of this great program.”
USAF Engineer
Hill Air Force Base
 Serving the Numerical Simulation community since 1989
Serving the Numerical Simulation community since 1989