
By Dr. Barna Szabó
Engineering Software Research and Development, Inc.
St. Louis, Missouri USA
The term “simulation” is often used interchangeably with “finite element modeling” in the engineering literature and marketing materials. It is important to understand the difference between the two.
The Origins of Finite Element Modeling
Finite element modeling is a practice rooted in the 1960s and 70s. The development of the finite element method began in 1956 and was greatly accelerated during the US space program in the 1960s. The pioneers were engineers who were familiar with the matrix methods of structural analysis and sought to extend those methods to solve the partial differential equations that model the behavior of elastic bodies of arbitrary geometry subjected to various loads. The early papers and the first book on the finite element method [1], written when our understanding of the subject was just a small fraction of what it is today, greatly influenced the idea of finite element modeling and its subsequent implementations.
Guided by their understanding of models for structural trusses and frames, the early code developers formulated finite elements for two- and three-dimensional elasticity problems, plate and shell problems, etc. They focused on getting the stiffness relationships right, subject to the limitations imposed by the software architecture on the number of nodes per element and the number of degrees of freedom per node. They observed that elements of low polynomial degree were “too stiff”. The elements were then “softened” by using fewer integration points than necessary. This caused “hourglassing” (zero energy modes) to occur which was fixed by “hourglass control”. For example, the formulation of the element designated as C3D8R and described as “8-node linear brick, reduced integration with hourglass control” in the Abaqus Analysis User’s Guide [2] was based on such considerations.
Through an artful combination of elements and the finite element mesh, the code developers were able to show reasonable correspondence between the solutions of some simple problems and the finite element solutions. It is a logical fallacy, called the fallacy of composition, to assume that elements that performed well in particular situations will also perform well in all situations.
The Science of Finite Element Analysis
Investigation of the mathematical foundations of finite element analysis (FEA) began in the early 1970s. Mathematicians understand FEA as a method for obtaining an approximation to the exact solution of a well-defined mathematical problem, such as a problem of elasticity. Specifically, the finite element solution uFE has to converge to the exact solution uEX in a norm (which depends on the formulation) as the number of degrees of freedom n is increased:
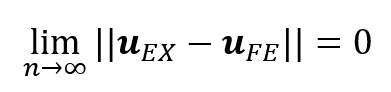
Under conditions that are usually satisfied in practice, it is known that uEX exists and it is unique.
The first mathematical book on finite element analysis was published in 1973 [3]. Looking at the engineering papers and contemporary implementations, the authors identified four types of error, called “variational crimes”. These are (1) non-conforming elements, (2) numerical integration, (3) approximation of the domain and boundary conditions, and (4) mixed methods. In fact, many other kinds of variational crimes commonly occur in finite element modeling, such as using point forces, point constraints, and reduced integration.
By the mid-1980s the mathematical foundations of FEA were substantially established. It was known how to design finite element meshes and assign polynomial degrees so as to achieve optimal or nearly optimal rates of convergence, how to extract the quantities of interest from the finite element solution, and how to estimate their errors. Finite element analysis became a branch of applied mathematics.
By that time the software architectures of the large finite element codes used in current engineering practice were firmly established. Unfortunately, they were not flexible enough to accommodate the new technical requirements that arose from scientific understanding of the finite element method. Thus, the pre-scientific origins of finite element analysis became petrified in today’s legacy finite element codes.
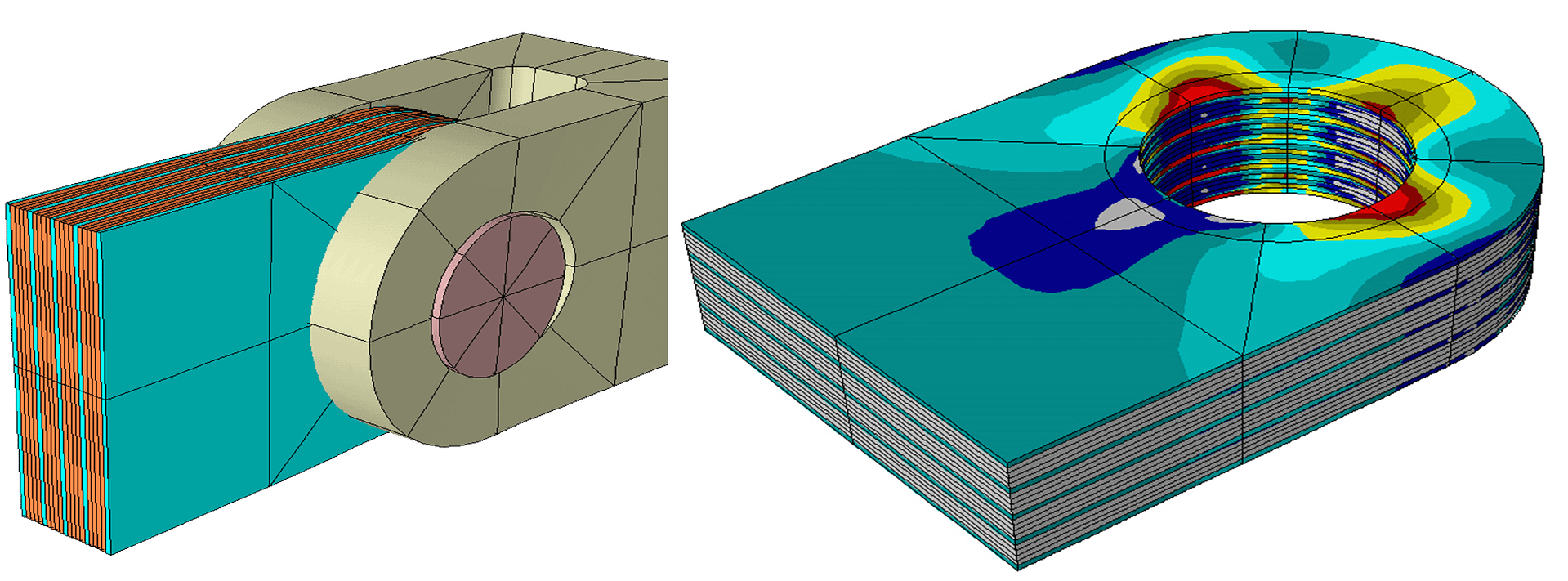
Figure 1 shows an example that would be extremely difficult, if not impossible, to solve using legacy finite element analysis tools:
Notes on Tuning
On a sufficiently small domain of calibration any model, even a finite element model laden with variational crimes, can produce results that appear reasonable and can be tuned to match experimental observations. We use the term tuning to refer to the artful practice of balancing two large errors in such a way that they nearly cancel each other out. One error is conceptual: Owing to variational crimes, the numerical solution does not converge to a limit value in the norm of the formulation as the number of degrees of freedom is increased. The other error is numerical: The discretization error is large enough to mask the conceptual error [4].
Tuning can be effective in structural problems, such as automobile crash dynamics and load models of airframes, where the force-displacement relationships are of interest. Tuning is not effective, however, when the quantities of interest are stresses or strains at stress concentrations. Therefore finite element modeling is not well suited for strength calculations.
Solution Verification is Mandatory
Solution verification is an essential technical requirement for democratization, model development, and applications of mathematical models. Legacy FEA software products were not designed to meet this requirement.
There is a general consensus that numerical simulation will have to be integrated with explainable artificial intelligence (XAI) tools. This can be successful only if mathematical models are free from variational crimes.
The Main Points
Owing to limitations in their infrastructure, legacy finite element codes have not kept pace with important developments that occurred after the mid-1970s.
The practice of finite element modeling will have to be replaced by numerical simulation. The changes will be forced by the technical requirements of XAI.
 Serving the Numerical Simulation community since 1989
Serving the Numerical Simulation community since 1989 








Leave a Reply
We appreciate your feedback!
You must be logged in to post a comment.