By Dr. Barna Szabó
Engineering Software Research and Development, Inc.
St. Louis, Missouri USA

A mathematician delivered a keynote presentation at an engineering conference some years ago. At the coffee break, following the presentation, a highly respected senior developer of a legacy finite element code, remarked: “I do not understand why the speaker was so worried about singularities. We never see them.”

In the context of the keynote presentation, singularities were understood to be properties of the exact solutions of mathematical problems approximated by the finite element method. Singularities occur in points where the exact solution lacks differentiability or analyticity. The remark, on the other hand, was in the context of finite element modeling where a numerical problem is constructed without considering the underlying mathematical problem. The remark highlights the lack of a common language between the pre-scientific notion of finite element modeling and finite element analysis, which is a branch of applied mathematics.

Why Do Mathematicians Worry About Singularities?

Mathematicians understand finite element analysis (FEA) as a method for obtaining an approximation to the exact solution of a well-defined mathematical problem, such as a problem of elasticity, cast in variational form. Specifically, the finite element solution u_FE converges to the exact solution u_EX in a norm (which depends on the variational form) as the number of degrees of freedom N is increased. An important question is, how fast does it converge?  For most practical problems, convergence is quantified by the inequality:

||\boldsymbol u_{EX} -\boldsymbol u_{FE}||_E \le \frac{C}{N^{\beta}}  \quad (1)

where on the left is the energy norm measure of the difference between the exact and the finite element solution (which is closely related to the root-mean-square error in stress), C and β are positive constants, and β is called the rate of convergence. The size of β depends on the regularity (smoothness) of u_EX and on the scheme used for increasing N. The details are available in textbooks, see (for example) [1].  The smoothness of u_EX is quantified by a positive number λ. In many practical problems 0 < λ < 1.

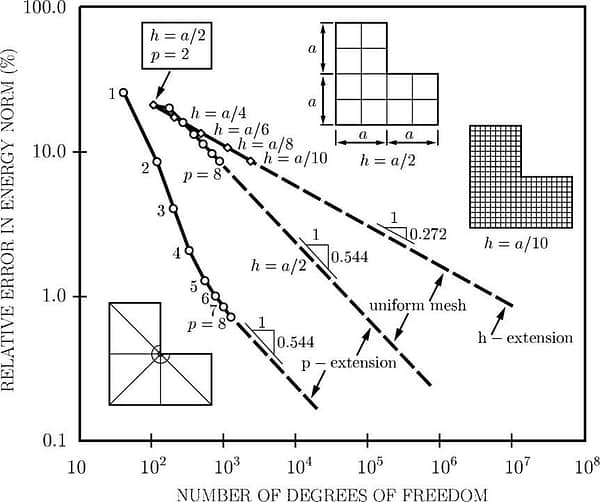
For instance, consider the two-dimensional elasticity problem on the L-shaped domain, a frequently used benchmark problem, where λ equals 0.544. This is a manufactured problem with a known exact solution, allowing for the calculation of approximation errors [2].

Referring to Figure 1, if uniform mesh refinement is used at a fixed polynomial degree (h-extension) then β = λ/2 = 0.274. If the polynomial degree is increased on a fixed uniform mesh (p-extension) then β = λ = 0.544. If p-extension is used on a mesh that is graded in a geometric progression toward the singular point then, for large N, we still have β = λ = 0.544, however, convergence is much stronger at small N values.

Assume that we wish to reduce the relative error in energy norm to 1 percent. If we increase the polynomial degree uniformly (p-extension), on a geometrically graded mesh then we have to solve less than 10³ simultaneous equations. In contrast, if we use a uniform mesh refinement and p = 2  (h-extension) then we have to solve about 10⁷ equations. The ratio is roughly 10⁴. It took less than one second on a desktop computer to solve 10³ equations. If we assume that the solution time is proportional to the number of degrees of freedom squared, then achieving 1% relative error with uniform mesh refinement would take 10⁸ seconds or 3.2 years. This shows that the errors of approximation can be controlled only through proper design of the discretization scheme, which involves taking the characteristics of the underlying mathematical problem into consideration.

Why Should Engineers Worry About Singularities?

If the solution of the underlying mathematical problem has singular points, as in the case of the L-shaped domain problem, then the goal of the computation cannot be the determination of the maximum stress. The finite element solution predicts finite values for stress, however, the predicted stress increases as N is increased. The error in the maximum stress is infinitely large even if the root-mean-square error in stress on the entire domain is negligibly small. This is illustrated in Figure 2 where the von Mises stress corresponding to the finite element solution on the 18-element geometrically graded mesh and p = 8 is displayed.

In engineering applications of the finite element method, small geometric features, such as fillets, are often neglected, resulting in sharp corners and edges. This may be permissible outside of the domain of primary interest, however, the quantities of interest within the domain of primary interest may be polluted by errors coming from singular points or edges [3].

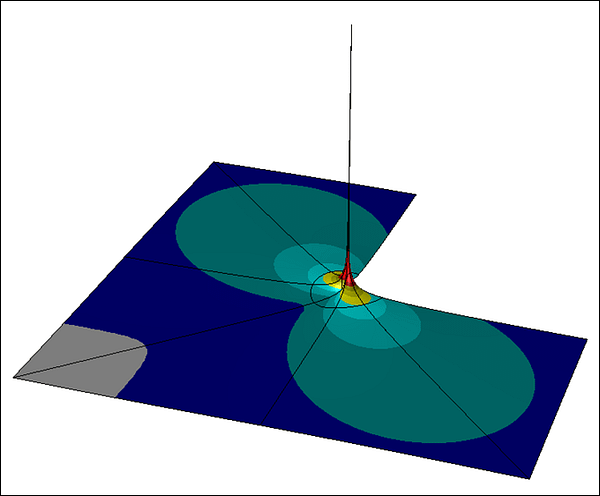
In this model problem, the singularity was caused by a sharp corner. Singularities can be caused by abrupt changes in material properties, loading, and constraint conditions as well.

Outlook

A high level of expertise is required for properly designing a discretization scheme. Experts take into consideration the information contained in the input data and use that information to estimate the regularity of the exact solution. This guides the design of the finite element mesh and the assignment of polynomial degrees.  Feedback information can be utilized to revise and update the discretization scheme when necessary [4].

Explainable artificial intelligence (XAI) tools can provide high-quality guidance in the design of the initial discretization, based on the information content of the input data, and in the management of feedback information. It’s essential, that these tools be trained on the scientific principles of finite element analysis.

References

Related Blogs:

• Where Do You Get the Courage to Sign the Blueprint?
• A Memo from the 5th Century BC
• Obstacles to Progress
• Why Finite Element Modeling is Not Numerical Simulation?
• XAI Will Force Clear Thinking About the Nature of Mathematical Models
• The Story of the P-version in a Nutshell